GAMES101 课程 3、4 记录 & 作业 1 题解
这两节的内容主要是变换,包括建模时的缩放、平移、旋转都属于变换,而当物体在三维空间中处于世界坐标系下,摄像机去观察的时候,我们需要从世界坐标系将物体变换到相机坐标系中,最后当物体最后呈现在显示器上时,又需要进行投影变换,因此,变换也是及其基础的两节内容。
Lecture 3 变换【二维与三维】
一、变换类型
- 模型变换【Modeling】
- 缩放【scale】
- 平移【Translation】
- 旋转【Rotation】
- 切变【Shear】
- 视图变换【Viewing】
- 3D 转 2D 的投影【Projection】
二、二维变换
这里的二维变换除了平移都是利用矩阵进行线性变换,做变换的时候我喜欢理解为,改变了物体所在空间坐标系的基造成了图像的变换,也就是基变换,忘了的话可以在 3Blue1Brown 的这期视频【线性代数的本质 - P13 基变换】重新回忆一下。
缩放【Scale】

非等比缩放镜像【Reflection】

缩放得到镜像将坐标以矩阵形式表达也就是
切变【Shear】
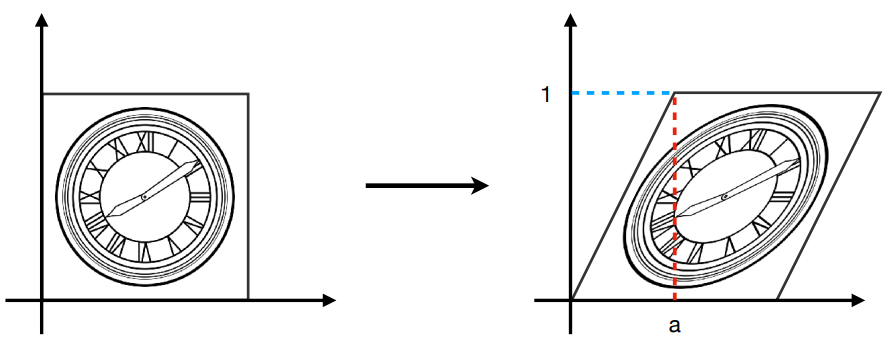
切变:想象是把 y 轴往右边拉了以后整个图像的偏移将坐标以矩阵形式得到
同理如果是偏转 方向的话:
旋转【Rotation】

旋转的矩阵推导将左图的点 和 带入上式
于是可以得到旋转矩阵 为
以上都是线性变换,都可以用以下矩阵形式表达:
平移【Translation】
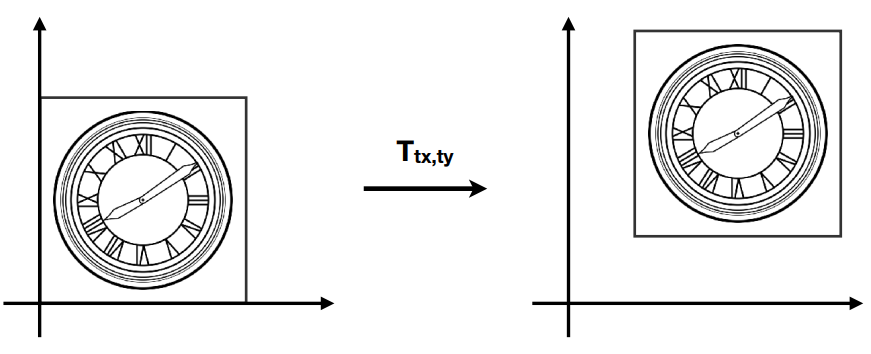
平移是非线性变换转换为矩阵形式就是
显然这样的形式和前面的线性变换不一致,为了方便平移这类非线性变换也能使用 的方式表示,我们引入齐次坐标的概念。
三、齐次坐标【Homogeneous Coordinates】
给二维的向量和点增加一个维度,这样就可以表示所有的变换了。
- 2D Point =
- 2D Vector =
对应的平移可表示为
对于点的齐次表示是增加 1,而向量是 0

点和向量的齐次坐标不同的原因
这样可以得到一个性质,两个点的坐标相加能够直接表示出两个点的中点。然后通过齐次坐标的形式,我们可以把仿射变换【Affine】都写成以下形式:
- 仿射变换【Affine】= 线性变换 + 平移
缩放【Scale】
旋转【Rotation】
平移【Translation】
逆变换【Inverse Transform】
逆变换就是反向变换,比如旋转一个角度,逆变换就是反着旋转回去,只需要左乘变换矩阵的逆矩阵就行,写作 。其中旋转矩阵是正交矩阵,旋转矩阵的转置就是他的逆矩阵。
组合变换【Composing Transforms】

如何通过变换得到这样一个的图像
一个变换可以通过不同的多个基本变换组合得到,比如上图的变换可以通过先旋转再平移得到,写作:
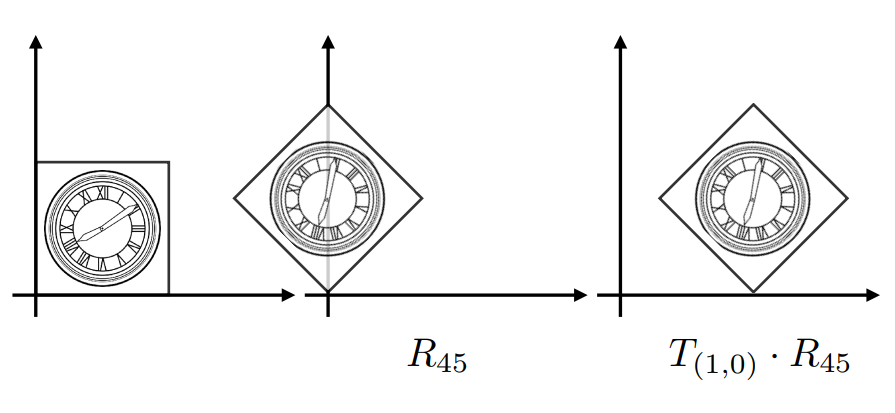
先旋转再平移
注意:矩阵乘法有结合律但是没有交换律,因此交换变换顺序得到的图像大概率都是不同的。
四、三维变换
三维变换和二维变换类似,这里做一个简单记录:
- 三维向量:
- 三维点: 或
缩放
平移
旋转
关于 轴旋转 角度
关于 轴旋转 角度
关于 轴旋转 角度
关于任意过原点的向量旋转
- 罗德里格斯旋转公式【Rodrigues' rotation formula】
于是一个三维的旋转可以被看作是一个基于 轴的旋转的组合,也被叫做欧拉角:
常被用于飞行模拟:Roll, Pitch, Yaw
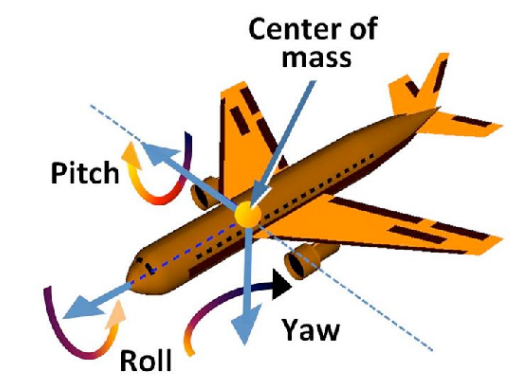
飞行模拟中的 Roll,Pitch,Yaw
Lecture 4 变换【模型、视图、投影】
观测变换是为了将三维空间中的物体变为二维,观测变换又分为视图变换和投影变换。
想象一下拍照的过程【MVP】:
- 模型变换【Model Transformation】:找到一个好的角度,摆放模型
- 视图变换【View Transformation】:找到一个号的角度设定相机
- 投影变换【Projection Transformation】:按下快门,将三维场景投影到二维相片上
一、视图变换【View / Camera Transformation】
视图变换就是把相机放在空间中某个位置来观察物体,所以这个问题可以转换为如何定义一个摄像机。如何定义一个相机,有三个部分:
- 相机位置【Position】:
- 相机观测方向【Gaze Direction】:
- 相机头顶方向【Up Direction】:
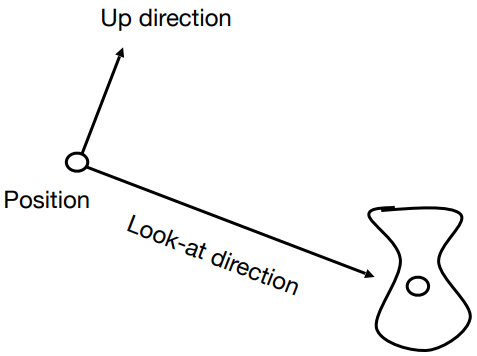
相机位置
通过相机空间观察物体,当相机和全部物体都在同时移动时是保持相对静止的,所以最后的成像也不会有改变,于是为了简便可以有两种方式:
- 以相机原点为坐标原点,变换所有的物体
- 以物体为原点,变换相机
课程里使用的是第一种方法,将相机固定在原点,朝向 轴,并让上方向为 轴方向。
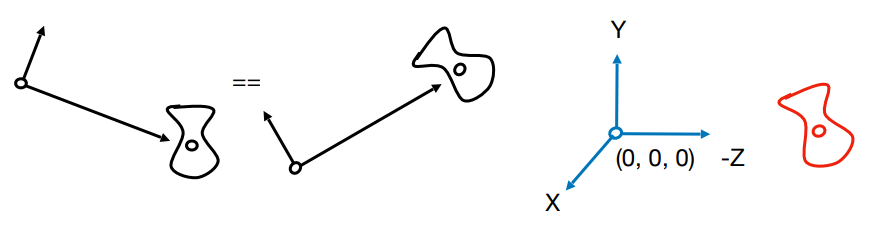
相对位置
将相机从任意位置移动到原点只需要几次仿射变换:
- 平移 到原点
- 旋转 到 轴
- 旋转 到 轴
- 旋转 到 轴
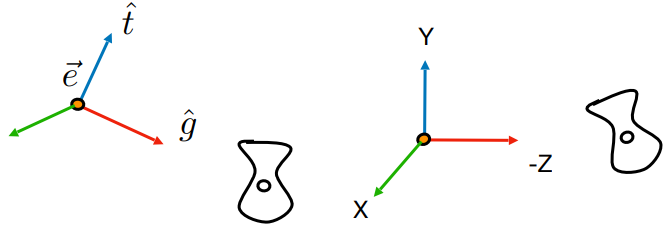
将相机移动到原点
用矩阵表示整个变换过程就是 :
平移 到原点:
旋转将三个轴与 轴对齐:这里比较麻烦的就在于,将轴旋转回原点是很复杂的,但是我们知道,旋转矩阵是一个正交矩阵,只需要先将坐标轴旋转到向量然后求逆矩阵【因为是正交矩阵所以结果就是转置】就可以得到旋转矩阵:
二、投影变换【Projection Transformation】
投影是将 3D 转为 2D 的过程,分为正交投影【Orthographic Projection】和透视投影【Perspective Projection】

正交投影【左】和透视投影【右】
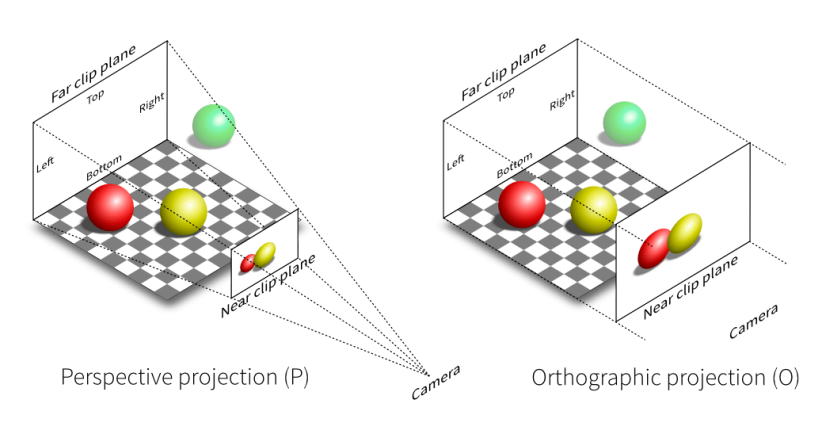
正交投影【右】和透视投影【左】
- 透视投影:成像效果更接近人眼,有近大远小的效果。
- 正交投影:假设视点无限远,看到物体的视野范围是一个长方体,物体的属性在成像上不会受到视角影响,常用于工程制图。
正交投影
正交投影的一种简单的理解方式:
- 相机位于原点看向 方向,上方向为 轴方向
- 把 轴丢弃
- 将所有的矩形通过平移和缩放规范化到
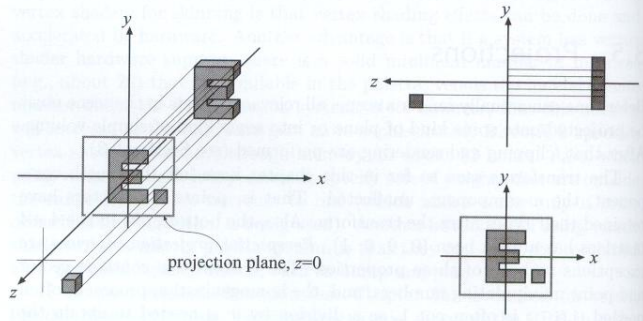
简单理解正交投影
正交投影的实现和上面的理解会略微不同,比如实现中正交投影就是把一个长方体 构成的空间压缩到一个 的立方体空间中。

正交投影的实现方式
注:,其中因为相机朝向是 所以
具体实现需要以下步骤:
- 把立方体空间平移到原点【空间中心与原点重合】
- 把空间缩放成
可以用矩阵的方式写作:
空间中立方体的中心点通过定义的六个方向值就可以得到 ,也就是:
然后是缩放空间,也就是按各个边长和最后规范化构成的比例缩放,因此 方向的缩放因子为:
则缩放矩阵为:
最后可得到正交投影矩阵为:
透视投影
透视投影和正交投影类似,步骤为:
- 把空间平移到原点
- 将截锥体空间压缩成长方体【压缩距离较远的平面】
- 将空间缩放为 的立方体【正交投影】

压缩截锥体空间为立方体空间
相比正交投影,透视投影有一个把锥体变换成立方体的步骤,我们可以把这个步骤写作 ,我们先了解这个变换的原理才能写出计算的方法:

截锥体转换到立方体的坐标计算方式
上图是 平面的截面, 代表立方体的 面 代表 面,通过,图中的点 在通过变换后会变为 ,我们可以写出如下等式:
同理对于 我们也可以得到 ,但是 方向不同,在透视变换的压缩中,点的 方向会发生一定程度的变化,因此在这里是 的状态,然后我们可以得到这样的关系:
对于 轴,由 得到, 其余 都为 ,同理求 轴可得:
第三行表示的是 方向的变化,其中我们知道最近点和最远中心点的 轴在变化后也是最近点和最远中心点,所以可以写出这样的关系【近平面任何点变化前后都不变,远平面只有中心点是不会变的】:
假设近平面的任意点都不会变:
同样带入 计算,因为结果与 无关,所以可以假设第三行的四个元素为
同理对于远平面的中心点:
联立上面的方程组可以得到:
于是整个压缩变换矩阵就是:
所以整个透视变换的矩阵形式就是 。
通常来说,在实际的工程中,我们通常并不会直接得到正交投影中的 和 的值,但是可以通过一些其他已经定义的东西计算出来,也就是 Field of view【FOV】 和 Aspect ratio【屏幕宽高比】。

FOV 和屏幕宽高比
FOV 分为 FovY 和 FovX 两个部分,结合屏幕宽高比就可以将 和 算出来:

用 FovY 和宽高比得到 l,r,b,t 值
以 FovY 举例,根据三角函数我们可以写出:
根据宽高比的定义,我们可以得到:
联立方程可以得到:
这样就得到了所有需要的值。
作业 1 题解
对于作业题解,这里按照 Game101 的规范都不会记录相关代码,不过其实网上一搜也能搜到很多了,主要记录一个解题过程。
本次作业主要是使用 CPU 模拟一个光栅化渲染的过程,其中我们需要对 main.cpp 中的函数进行补全:
get_model_matrix(float rotation_angle):- 将输入的
rotation_angle值换算成为弧度值,并创建一个旋转矩阵作为输出,交给set_model函数传给光栅化器。
- 将输入的
get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar):- 需要返回的是一个投影矩阵,根据输入的
eye_fov,aspect_ratio和zNear,zFar可以得到l, r, t, b的值就可以直接构建得到。
- 需要返回的是一个投影矩阵,根据输入的
渲染得到的结果